3月 1-10日
1(金)
ABC103 D Island War: 整理すると,区間を貫く直線を用意し,全部の区間を貫きたい.この直線の数を最小化することになる.これはスケジューリングっぽくやればよくて,後ろでソートして前から詰めればできる. submission
ABC102 D Equal Cut: まず切る場所を全探索する.切り分けた左右2つBC,DEについて同じ問題を解く.連続列を差分が小さくなるように2つに分割する.
どうして独立した2つのブロックBC,DEを更に分割する際にそれぞれの差分を最小化すればいいかというと,適当な状態で(BCの最小値)<(DEの最大値)となっているとする.
それぞれの差分を小さくすれば最小値と最大値を近づけることになるので嬉しい.
差分を小さくするには三分探索が動き的に適していそうで,これをすればよい.
submission
このスタイル慣れればかなり良さそうなのでこれでやっていきたい.
templateから概要解説の文字を消した.
ところでindeedの新卒年収が話題になっていた.
2(土)
ライブラリの整備をしていた.
RollingHash: hashbaseの$B$はランダムに選ぶべきで,十分大きな$MOD$に対しては、ランダムに選べば長さ$n$の入力に対して衝突の確率は多くとも$ \frac{n−1}{MOD}$であることを知った.Link
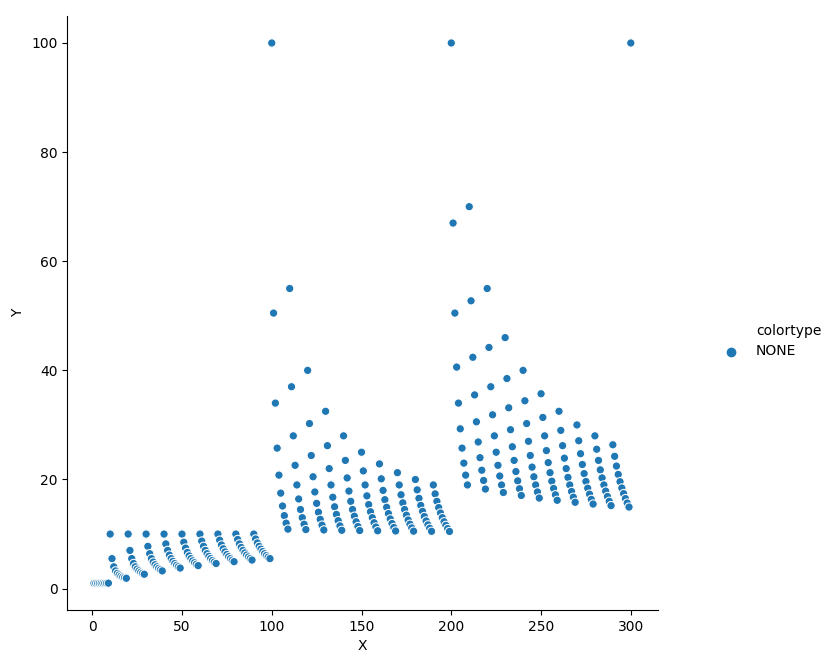
2D可視化をpythonのseabornで書いた.
値にタグを付けると色や形で違いがわかって結構いい感じ.
3(日)
ABC101 D Snuke Numbers: これ確かICPCお疲れ様&ISUCON頑張ろう会のときに見せられて一瞬では解けなかった問題な気がする.実験として↑みたいな可視化をするとわかりやすくて,*999みたいなやつが候補になっていることが分かる.さて,*の最大値はどれぐらいなんだろうということがわかれば,全列挙しても間に合うかどうかの検討がつく.
候補の数のうち,$\displaystyle \frac {val}{f(val)} > \frac {val2}{f(val2)}$ $(val < val2)$である$val$が不適であり,これを式で抑える.
$val = a*10^n -1$と書ける.$f(val) = b$として,$val2 = (a+1)*10^n-1. f(val2) ≧ b+1$
適当に解くと$p>b$っぽくなる.$b$の最大値は135なので,$p>135$のとき$val$がSnukeNumberではないと言える.
そこで,$[0,135)*10^n - 1$を列挙し,実際にチェックする.$n≦15$であることがわかっているので,適当にチェックすることで制約下のSnukeNumberを全部得ることができる. submission
思考がほぼほぼ一緒だった(!?)
ABC120に参加:(18th) A問題とB問題の日本語の理解に時間がかかった(え?) もっと速く解けた気がする.
ABC120 D Decayed Bridges: 前からは不可能(ダイコネがあればできる)なので後ろから見る.
最後の値は$N*(N-1)/2で$,島をつなげるごとにつなげる左右の島のサイズがわかれば,答えからサイズの積を引いていけば良い.島のサイズとつなげる動作はUnionFind等で簡単に実現できる.submission
ところで
を見て差を感じた...potentializedUFでは確かにアーベル群が乗るので,xorもできる.が,あまり制約系というイメージがなくて,そういう些細なことから考察に差が生まれている気がした.UnionFind, 変数x_1, x_2, ..., x_nに対して x_{ai} xor x_{bi} = ci の制約の集合を解くのにも使えるし、x_{a1} - x_{b1} = c1 制約の集合を解くのにも使える
— drafear (@drafear) March 3, 2019
4(月)
筋トレした.今週も頑張るぞ!
ABC100 D Patisserie ABC: 絶対値が面倒なのでとりあえず8個全部試せば良い.N個からM個取るのはdpでできるので書く.submission dpいらないね.
ABC099 D Good Grid: まず$(i+j) mod \space 3$で要素を分離できる.分離した要素について,色が全部$c_i$となる違和感の和は$O(NC)$で求めることができる.
あとは,3つのグループについて異なる色を割り振ればよく,これは$O(C^3)$でできる.submission
ABC099 C Strange Bank: dpで殴る.$O(NA)$ (Aは異なる金額の個数で15ぐらい) 1を$6^0$,$9^0$とみれれば全探索もできる.(思いつけば) submission
ABC098 D Xor Sum 2: 連続部分列のsumとxorが一致している区間を伸ばすことを考える.一致している状態に足して一致しなくなった後に更に足すと一致するようなケースは存在しないことが分かる.(xorの桁独立とsumの繰り上がりから) よってしゃくとり法で求めて良い. submission
ABC 097 D Equals: 何度も移動してもいいので,連結された関係を満たす任意の数列を構成することが可能である.よって$a_i=i$にできるかどうかの判定は,$a_i$を移動させるグループ内に$i$が含まれるか?という質問に答えればよく,これはUnionFindでできる.submission
ABC 096 D Five, Five Everywhere: 5つ選んだときに合成数であるということはなにかの倍数になっている.
つまり,剰余が0になるということである.3の倍数だと壊れるので5の倍数で考える.$5n+1$を5つ集めると5の倍数になる.
素数のうち5で割ると1余る数を55個列挙してみると,55番目は1381らしいので余裕.submission
yukicoder 737 PopCount: 典型桁dpっぽい.組み合わせと総和を持って再帰すれば簡単に書ける.
ただしpopcount(x)が面倒なので,再帰関数を$f(S,c):=S$以下の数のうち,1の数が$c$個である組み合わせとその総数とし,$\sum f(S,c)*c$を求めれば良い.
submission
他の人のsubmissionを見ているとなんか再帰で桁dpを書くのは少数派みたいな感じがしていて怖い.
5(火)
RUPC2019day1に参加 楽しいセットでした…!
C: シュミレーションを書くとなんかキレイな図になり,正しそうということで埋め込む.(あとで証明した)
D: インタラクティブは二分探索か天才になる.今回は二分探索.$1,2,3,..,9$から$2^i$個辺を張って$2^i$個辺を張らないをすれば二分探索できる.9回にしないと特定パートでWAになる.(これをやっていないけどグラフをK回出力してREしていた)
E: LISをセグ木で書いたことがあれば書ける.(LIS長,重み)で区間$[0,a_i)$max取得,updateができれば良い.
G: フローかなと思ったけど最大カットになってしまい悲しい.$2^3$ぐらい状態数を増やせばDPできそうかなと考えていたけど結局時間内に書き上がらなかった.
蟻本のGCJ4章にこんな問題があって,二部グラフのOR制約はPSPでも解けてしまう.これ実家といっている人が多くてかなり怖い.
F: てんぷらさん&drkenの解説が天才.でも王道な気がする.
絶対値記号を外すと$a_i-i$ or $i-a_i$になる.+が$N$個で-が$N$個になり,この場合$2N$個の項の総和を最大化することになる(大小のみ考慮すれば良い).
それぞれの$(a_i,i)$の大きい方を$+$,小さい方を$-$に割り振る.
次を考える.”“$A,-B(A<B)$が存在すれば,これを$B,-A$にするswapが存在する.””
$(a_i,i),(a_j,j)$について考えた時,まず負で大きいものを選択するが$(+,-),(-,+)$からは大小の$+-$のルールから絶対に選択できないことが分かる.
$(+,-),(+,-)$からは選択可能で,$B,-A$になる組が必ず存在することを示すことができて,$2*|A-B|$だけ先の$2N$個の総和を大きくすることができる.最大$M$回大きくならなくなるまで試せば良い.
6(水)
RUPC2019day2に部分的に参加 後ろの問題はおもしろいので後で解く. H: 昨日のGと一緒どころかこっちのほうが簡単.PSPで解く.
L: 結局$subset \space G$の積が $mod \space P$ で$A$になるかを判定したい.どうすればいいのかな なんか位数で解けるっぽい 参考
M: 文字列は解けそう.SAやLCPは当然のように使うけど,間の文字が邪魔だった.
7(木)
筋トレ.
ABC095 D Static Sushi: 0から時計/反時計回りで移動したときに,最大利益を得ることができる点を全探索すれば良い.
これは累積和を持つだけでできる.一度折り返すパターンもあり,これはsegtreeでmaxをもってくると楽.(なお実装…)
submission
8(金)
ABC094 D Binomial Coefficients: パスカルの三角形をみる.$comb(max(a_i),x)$を考える.$x$は$a_i/2$に近いほど$Comb$は大きくなる.
$max(a_i)$でない数が最大値を取るとすると,それを達成するもう1つの数を$max(a_i)$に適用したほうが大きな値になる.これを探せば良い. submission
ABC093 D Worst Case: 要復習.$AB$以下になる$ab$の個数を発見したい.$a=1$としたとき,$b=AB-1$となることから,この区間の数字のみを考える.
また,$b$はこれよりも小さくても成り立つ.$[1,2,3,..,AB-1]*[AB-1,AB-2,…,2,1]$としたとき,中央の値が$AB-1$を超えないような区間のサイズが答えとなる事がわかる.
これは二分探索等で簡単に見つけることができる.$A,B$を取り除いたときはサイズ-1となるだけである.
$A=B$の場合のみ答えが違うので注意.
submission
ABC092 D Grid Components: 二領域に分けて置くだけ.submission
9(土)
知り合いにストレッチとヨガのトレーナーがいるのでストレッチの正しいやり方を教えてもらってきた. 筋トレ睡眠ストレッチとすごい健康になっていく…
ABC121に参加.2th 嬉しい.が,初心者コンテストに出るのは良くないという気がしている(常に勉強になるのでせめてOpenコンテスト作って欲しい…)
見にくいんだけど,後輩の勧めで所属で宣伝をした.名大でプログラミングしたい人は連絡ください.
ABC121 D XOR World: [0,X]の累積xorを高速に求める事ができれば良い.2進数では下から周期的なので各桁の値を見れば分かる. submission
10(日)
筋トレ.
新歓用?というかネット検索用の雑記事を作った.
キラキラさせると一回来てもう一生来ない人が来てしまうのでいい感じに篩にかける文章にしたつもり.
あと大学生の自由研究さんの記事に載せてもらえないかお願いしてみた.
載せてくれるといいな.
ABC091 C 2D Plane 2N Points: 二次元にplotするといい問題の一例.X昇順でみて,覆う方が最大のyを取っていけば良い.ARCの合コン大作戦もこれっぽくやる.submission
ABC091 D Two Sequences: 難しいけど好き.$a_i+b_j$を集計して,2進数でk bit目の数が偶数か奇数かを知りたい.
k bit目について1であるということは$a_i+b_j$をmod $2^{k+1}$で見ても問題ない.
$2^k ≦ ai+bj < 2^{k+1}$ であればよく,$a_i$の場合分けで解ける.式でやるとミスるので線分で考えるとかなり間違えにくい.submission