今までは全ての解いた問題全部の概要と解説をGitHubに,タグや難易度,復習問題管理をspreadsheetに書いていた.
復習問題管理以外に価値はないことがわかってきたので解法メモを書いておくべきと思ったものは時系列順にここに全部書くことにした.
競技プログラミング以外の話も書くかも.
2月
卒研をしていた.最初はROSを触っていたけど最終的に点群ライブラリであるところのPCLのドキュメントを読みまくってライブラリを改造するみたいなことをしていました. 疲れた.あとアカデミックの人の文章力に驚いた.足向けて寝れない.(これは罠で誰にも足を向けて寝られない)
2月下旬
卒研が終わったのでDockerの本と並行して離散凸解析を読み始めた.マトロイドっぽいものも出てきて2色の最小全域木とかを雰囲気をせず解けるようになった.
あと友達に誘ってもらってCAのBaseCampに行ってきた.各セッションはそこまで学びがなかったけど社長のファーストキャリアの重要性の話には考えざるを得なくなった.行ってよかった.
なんか懇親会に変な人がたくさんいて楽しかった.
翌日リクルートテクノロジーズのフロントエンド高速化コンテストに参加してきた.チームメイトが優秀で優勝した.特に何も貢献できた気がしないのでホテルで全部再現したりして知識をつけ直した. フロントエンドへのイメージがガラリと変わって楽しかった.
得た知見でCodeforces Problemsを若干高速化した.service workerを入れると更に速くなるっぽいけどまだできていない.issueとして立ててあるのでいつか必ずやる.
28日(木)
2ヶ月ぶりに競技プログラミングをやる時間と気持ちを得たので再開した.
3月はABC*3+ARC*2をやっていきたい
ABC119 D LazyFaith: ソート済みの列に対して,X->s->tの移動経路は二分探索できるのでOK.番兵をいれるといい感じにできるのは見落としていた…(実装初心者) submission
ABC118 D Match Matching: ちょうどN本つかってできる値の最大値を見つけたい. dp(n):=n本マッチ棒をつかってできる最大値として, dpの型をstringにすればよい.stringは辞書順でやってしまうので,O(N)の比較関数を書いて対処する.O(N^2) submission
ABC117 D XXOR: まずXORの和なので2進展開したときに各桁独立してみて良い.X以下の数字を全探索する際,独立していることからlogX回,最適な0/1を選択していけば良い.この際X未満かどうかわからないとXよりも大きい数字をつくってしまうので,桁DPでよく使うlessフラグをもってやれば良い.O(N*logX) submission
ABC116 D Various Sushi: 寿司を種類ごとにまとめてやると種類で全探索できる気がした.これだとdpになりそうで,O(N^2)を下回ることはできなさそう. 種類で見ないように方針転換する.ネタの美味しさを降順でとっておく. このとき,交換をすることで種類を増やせば最適解にあたりそう. ネタの種類を増やすので,減らさないほうがいいのはそれはそう(降順に取っているので減らすことに旨味が0)各種類のネタで2番目以降の美味しさを全部保存しておき,その最小値を取れば良い.これはheap等で簡単に実現できる.(なんか全部multisetでいい気がしてきている(どっちもとれるので)) submission
ABC115 D Christmas: 再帰的につくれらたバーガーから,端からX枚に含まれるPの数をカウントする.あるレベルのバーガーに含まれるB,Pの総数と,Pのみの総数はレベルが低いものから線形で数えることができる. 実際に木を下るさいにこれらの情報をもとに移動する.あるLV-1バーガーよりもXが大きい=下る必要がない=計算を端折れる より,バーガーでできる木の高さまでしかたどる必要がない.O(N) submission
ABC114 D 756: 約数が75になるとは,N!に含まれる素因数の個数p_iについて,75=Π(p_i+1)が成り立つことである.これは場合分けやdpでできる. 場合分けのほうが計算量が少ないが,楽にやるならdpだと思う.(ただし思いつかないといけないのでこれは精進…) submission1 submission2(dp)
ABC113 D Number of Amidakuji: 上の段からdpすれば良さそう.ある段の横線について,validの条件を満たすものが存在し,これらの遷移でdpをしていけばよい.validの条件を満たすものはO(2^w)で全列挙しても間に合う.ちゃんと読んでなくて2^(W-k)とかが遷移に生えて,コーディングが終わってから気がついた.ちゃんと読もう.(読んでないのはスタートラインにすら立てておらず本当に最悪なので) submission
ABC112 D Partition: まず素因数分解をする.a_iそれぞれがpの倍数である時,gcdがpとなる.したがってp*(N+k), (k≧0)となるMの分解があるかを見て,あるならpの最大値をansとして保存していけば良い.O(√M)submission
ABC111 D Robot Arms: d_iが与えられたとして,これらが全ての配置をみたすかどうかはx+yのパリティを見れば分かる.[これ気がつくの結構難しいと思うけどどうすればいいのかな] というのは,x,yのどちらかにd_iを使う際,x+yの偶奇は変わらないので,全てのx+yのパリティが一致している必要がある. パリティが一致していて,奇数の時を考える.アームは2べきで作ると良さそうというのは直感で分かる.配置可能な領域を書くと次の白点のようになる.
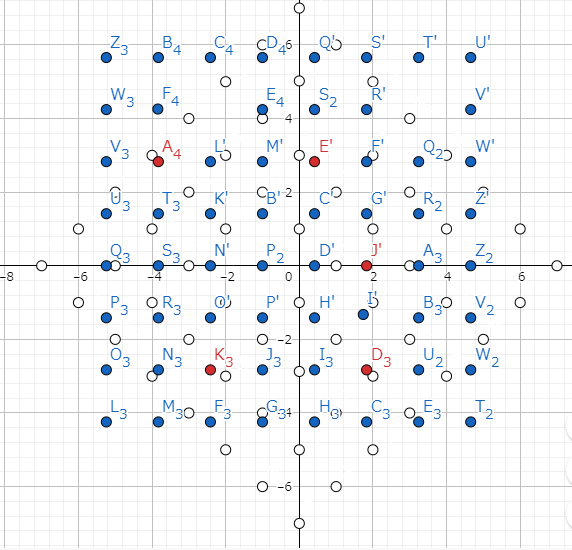
これはパリティも配置可能な領域も見れていなかったので要復習. 配置可能な領域は実験だけど,まずパリティに気がつく必要があって,これは本当にどうすればいいのかわからない.submission
ABC110 D Factorizetaion: これいつかのARCになかったかい..https://atcoder.jp/contests/arc004/tasks/arc004_4 素数ごとに見て良い.素因数分解して,各素数をN個に複数個割り振ってもいい組わせなので,nCr(N,N-1+p_cnt)の積を取れば良い.submission
ABC109 D Make Them Even: 奇数の場所を移動させていけば最後には1or0個になる事がわかる.一筆書きで移動できればよく,これを実装すれば良い.submission
ABC108 D All Your Paths are Different Lengths: 2べきでやるのは当然.グラフを変に構築するのは筋が悪い.(いつもそうだよね) N-1=$\sum 2^k$ のときは S-(1,0)-[1]-(2,0)-[2]-(4,0)-[3]…と繋げば良い.(括弧は辺の値) ではNがそうでない場合はどうすればよいか.$\sum 2^k$ で小さい方から連続して選択するとそれらの値は1から連続していることを利用する. N-1=$\sum 2^k$ + Pのとき,Pを$\sum 2^i$ の集合に分割してしまえば良い.すると,(0,1,2,3,4,5,6,7)[+128] + (0,1)[+136] みたいにできる. 実装は結構適当にできる. 連続している値を利用するのがポイント.submission
ABC107 D Median of Medians: 中央値は面倒なのでX以上の値が列の過半数に置き換える!(素振り)
すると問題を次のように言い換える事ができる.
- X以上の値が過半数含まれる連続部分列の総数は?
- また,これの総数が連続部分列の数の過半数を占めるか?
1はX以上を1,X未満を-1とした列の累積和でcsum(R)-csum(L)≧0をあるRについて高速にLを取得できれば良い.これはBITでできる. 2は1で求まった個数について,N(N+1)/2の半分,N(N+1)/4以上であれば良い. 最初の二分探索パートからO(Nlog^2N)で解ける. これはCFでもTCOでも出ていたので解けないとダメそう. csum(R)-csum(L)>0とかcsum(R)-csum(L)≧0はX以下か,X以上かによるので,その都度ちゃんと確認する.submission
ABC106 D AtCoder Express 2: DQueryの弱い版.クエリと線分をRでソートする.あるRについて,線分のLに+1して,クエリは[L,R]の総和を見れば良い.これはあるRについてのあるあるっぽい.永続でもまあ良い.
制約が弱いので,L,Rを二次元にplotしてもよい.すると二次元領域に点を加え,正方形の総和を見ることになる.これは適当なデータ構造や前処理をいい感じにやることでできる.submission
ABC105 D Candy DIstribution: 区間和がmod M で等しいような数を数え上げれば良い.例のごとくprefixsumを持つ.するとindexR(これはprefixsum)にたいして,csum(R)-csum(L) = 0(mod M)であるものを数えることになり,これはmapでO(NlogN)でできる.submission
ABC104 D We Love ABC: これ結構時間がかかった.
ABBBBBCCみたいなのを考える.Cを見つけたときに,どのBを選んでも良い.これはオートマトンのdpっぽくみるとABCが2番目まで完成しているときに,3番目を選ぶ動作になる.(nx(3)+=dp(2))
すると他の遷移も見えてきて,ある文字が来た時,stepさせてもいいし,stepさせないということもできる.(後でstepすれば良いため)
?のときは当然全部できて,stepしないパターンも3種類ある点に注意.
結局,ABCとなるように3つ選択することが大事で,dpも選択した状態をもっていると考えるとかなり自然.
これ50分ぐらいかかったので要復習.
submission
最後に
2月は筋トレと睡眠と卒研を頑張った.3月は競技プログラミングを無限にやりたい.あといろいろな人に勧めてもらったことをやっていきたい.