問題概要
How to Create a Good Game
正の重み付きDAGが与えられる。
0からN-1への最長距離を変えないようにそれぞれ辺の重み$c(u,v)$を$0$以上の整数だけ増やす。
最大でどれだけ増やせるか。
$N\leqq10^2$、$M\leqq10^3$、$c(u,v)\leqq10^3$
解法
まず $edge (u,v)$の追加可能な最大値を$a(u,v)$、ある頂点$v$における最長路の長さを$d(v)$とする。
このとき与えられる$E$本の辺についての情報は次のように表せる。
$$ d(v) \geqq d(u) + c(u,v) + a(u,v)$$
これは変数と定数にわけることができて、
$$ (d(u) - d(v)) + a(u,v) \leqq -c(u,v) $$となる。
また、最長路を$D$として、 $d(N-1)- d(0)\leqq D$であるから、これら$E+1$本の式を用いて線形計画問題を表すことができる。
目的関数: $\displaystyle Maximize c*x$ ,
$c = \{0 ,…,0 ,1,…,1\}$ ($0$が$V$個、$1$が$E$個)
$x = \{d(0),…,d(N-1),a(e(0)),…,a(e(E-1))\}$
$s.t:$
$$
\begin{eqnarray}
\left(
\begin{array}{ccc|cccc}
1 & \ldots & 0 & 1 & 0 & \ldots & 0 \\
0 & \ldots & -1 & 0 & 1 & \ldots & 0 \\
\vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\
1 & \ldots & -1 & 0 & 0 & \ldots & 1 \\
\hline
-1 & 0 & 1 & 0 & 0 & 0 & 0 \\
\end{array}
\right)
\left(
\begin{array}{c}
d(0) \\
\vdots \\
d(V-1) \\
\hline
a(e(0)) \\
a(e(1)) \\
\vdots \\
a(e(E-1)) \\
\end{array}
\right)
\leqq
\left(
\begin{array}{c}
-c(e(0)) \\
-c(e(1)) \\
\vdots \\
-c(e(E-1)) \\
\hline
D \\
\end{array}
\right)
\end{eqnarray}
$$
$$ \forall v,d(v) \geqq 0 $$
$$ \forall i, a(e(i)) \geqq 0 $$
(いわゆる$Ax\leqq b$の形、$A$は$E+1$行$V+E$列、$x$は$V+E$行$1$列)
定式化できると高速なSimplex法でも解けそうだが、ここでは双対をとって問題を解く。
双対をとると、次のように変形される。
先の$b$を用いて
目的関数: $\displaystyle Minimize b^t*y$ ,
$s.t:$
$$
\begin{eqnarray}
\left(
\begin{array}{cccc|c}
1 & 0 & \ldots & 1 & -1 \\
\vdots & \vdots & \ddots & \vdots & \vdots \\
0 & -1 & \ldots & -1 & 1 \\
\hline
1 & 0 & \ldots & 0 & 0\\
0 & 1 & \ldots & 0 & 0 \\
\vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & \ldots & 1 & 0\\
\end{array}
\right)
\left(
\begin{array}{c}
y(0) \\
y(1) \\
\vdots \\
y(E-1) \\
\hline
y(E) \\
\end{array}
\right)
\geqq
\left(
\begin{array}{c}
0 \\
\vdots \\
0 \\
\hline
1 \\
1 \\
\vdots \\
1 \\
\end{array}
\right)
\end{eqnarray}
$$
$$ i(0\leqq i\leqq E), y(i) \geqq 0 $$
$b^t*y$ は$D*y(E) + \displaystyle \sum_{i}^{E} -c(e(i))*y(e(i))$である。
目的関数は最小化であり、制約さえなければじゃぶじゃぶ$y(e(i))$を大きくしたい。
これと非負の制約式から双対問題は最小費用流のようなものを感じ取る。僕は感じ取れなかった。
目的関数は辺の値*なにか0か1以上の値を取る変数である。
制約式の上から$V$本について正のものの総和を頂点への流入量、負のものの総和を流出量とみればこれは最小費用流の定式そのものである。
制約式の下$E$本については辺についての流量が1以上と見ることができる。
最小費用流だけど簡単なものとは違って流量の指定はなく、制約を満たせばどれだけでも流してよく最小化できるなら流せるだけ流せばよい。
したがって負辺あり、下限制約あり、流量が決定していない最小費用流とみなせる。
これらはすべて解決可能である。以下その方法の参考を記す。
- 負辺ありの最小費用流: 始点$s$についてのポテンシャルのみ、BellmanFord法で求めることであとはいつもどおりのDijkstra法でポテンシャルを取ればよい。
- 下限制約ありの最小費用流: 最大流のように変形を行うことができるがもう1辺を上手に張れば良い参考:蟻本第二版p.204。
- 流量が決定していない最小費用流: 今双対問題の最小値を求めたいのでじゃぶじゃぶ負のpathに流したい。つまりpotential[t]<0でなくなったとき計算を終了させればよい。
また、目的関数と制約から$d(N)$を新たにおいて、元あるグラフのコストを負に反転させ頂点$N-1$から頂点$N$にコスト$D$の辺を張った状態で、下限制約1の最小費用流とみなすことができる。
サンプル1の変形後
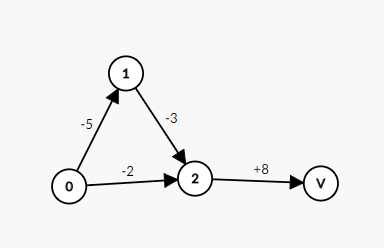
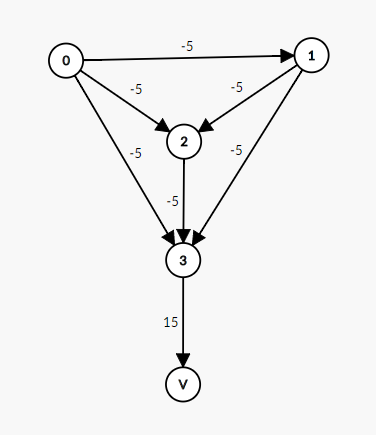
ソース
#include <bits/stdc++.h> using namespace std; using LL = long long; using VL = vector<LL>; #define SZ(a) int((a).size()) #define FOR(i, s, e) for (int(i) = (s); (i) < (e); (i)++) const int INF = 1e9; const LL LINF = 1e16; typedef long long PD_Type; const PD_Type PD_INF = 1e9; const PD_Type inf = 1e6; struct Primal_Dual { typedef pair< PD_Type, int > pii; struct edge { int to, rev; PD_Type cap, cost; edge() {} edge(int to, PD_Type cap, PD_Type cost, int rev) :to(to), cap(cap), cost(cost), rev(rev) {} }; vector< vector< edge > > graph; vector< int > prevv, preve; vector< PD_Type > potential, min_cost; Primal_Dual(int V) : graph(V) {} void add_edge(int from, int to, PD_Type cap, PD_Type cost) { graph[from].push_back(edge(to, cap, cost, (int)graph[to].size())); graph[to].push_back(edge(from, 0, -cost, (int)graph[from].size() - 1)); } void add_edge_limit(int from, int to, PD_Type capLB, PD_Type capUB, PD_Type cost) {// これ add_edge(from, to, capUB - capLB, cost); add_edge(from, to, capLB, cost - inf); } PD_Type min_cost_flow(int s, int t) // dont need flow { int V = graph.size(); PD_Type ret = 0; priority_queue< pii, vector< pii >, greater< pii > > que; potential.assign(V, PD_INF); // ! preve.assign(V, -1); prevv.assign(V, -1); potential[s] = 0; //一回だけbellmanfordで最初のポテンシャルを求める FOR(k, 0, V) { FOR(i, 0, V) { FOR(j, 0, (int)graph[i].size()) { edge &e = graph[i][j]; if (e.cap == 0)continue; potential[e.to] = min(potential[e.to], potential[i] + e.cost); } } } PD_Type f = PD_INF; while (potential[t] < 0) { // ! min_cost.assign(V, PD_INF); que.push(pii(0, s)); min_cost[s] = 0; while (!que.empty()) { pii p = que.top(); que.pop(); if (min_cost[p.second] < p.first) continue; for (int i = 0; i < (int)graph[p.second].size(); i++) { edge &e = graph[p.second][i]; PD_Type nextCost = min_cost[p.second] + e.cost + potential[p.second] - potential[e.to]; if (e.cap > 0 && min_cost[e.to] > nextCost) { min_cost[e.to] = nextCost; prevv[e.to] = p.second, preve[e.to] = i; que.push(pii(min_cost[e.to], e.to)); } } } if (min_cost[t] == PD_INF) return -1; for (int v = 0; v < V; v++) potential[v] += min_cost[v]; PD_Type addflow = f; for (int v = t; v != s; v = prevv[v]) { addflow = min(addflow, graph[prevv[v]][preve[v]].cap); } f -= addflow; ret += addflow * potential[t]; for (int v = t; v != s; v = prevv[v]) { edge &e = graph[prevv[v]][preve[v]]; e.cap -= addflow; graph[v][e.rev].cap += addflow; } } return ret; } }; LL N, M; LL ans = 0LL; int main() { cin.tie(0); ios_base::sync_with_stdio(false); cin >> N >> M; int S = 0; int T = N; Primal_Dual F(T + 1); vector<PLL>Gr[110]; FOR(i, 0, M) { int a, b, c; cin >> a >> b >> c; F.add_edge_limit(a, b, 1, PD_INF, -c); Gr[a].push_back(PLL(b, c)); } VL dist(N + 1, 0); FOR(i, 0, N) { FOR(j, 0, SZ(Gr[i])) { dist[Gr[i][j].first] = max(dist[Gr[i][j].first], dist[i] + Gr[i][j].second); } } F.add_edge(N - 1, N, INF, dist[N - 1]); ans = F.min_cost_flow(S, T) + M*inf; cout << ans << "\n"; return 0; }
Mathjaxは簡単に使えるのではてなブログ並みに消耗しなくなった。